ORIGINAL ARTICLE

https://doi.org/10.5005/jp-journals-10025-1177
International Journal of Keratoconus and Ectatic Corneal Diseases
Volume 8 | Issue 1 | Year 2019

Clinical Evaluation of a New Approach for IOL Power Calculation in Keratoconus

Vicente J Camps¹, Ramy R Fikry², Veronica J Mateo³, Fady E Labib⁴, Esteban Caravaca-Arens⁵, María T Caballero⁶, David P Piñero⁷

^1,3,5–7Department of Optics, Pharmacology and Anatomy, University of Alicante, Alicante, Spain
²Opthalmology Department, Cairo University, Cairo, Egypt
⁴Al Watany Eye Hospital, Cairo, Egypt

Corresponding Author: Vicente J Camps, Department of Optics, Pharmacology and Anatomy, University of Alicante, Alicante, Spain, Phone: +34 965903400, e-mail: vicente.camps@ua.es

How to cite this article Camps VJ, Fikry RR, Mateo VJ, et al. Clinical Evaluation of a New Approach for IOL Power Calculation in Keratoconus. Int J Kerat Ect Cor Dis 2019;8(1):1–6.

Source of support: David P Piñero is supported by the Spanish Ministry of Economy, Industry, and Competitiveness within the program Ramón y Cajal, RYC-2016-20471

Conflict of interest: None

ABSTRACT

Purpose: To obtain an expression of the adjusted IOL power (P_IOLadj) in keratoconus eyes associated with minimal errors in IOL power calculation.

Materials and methods: This retrospective study included a total of 25 eyes of 25 patients with ages ranging from 20 years to 76 years. The following IOLs were implanted: Acrysof IQ Toric, Acrysof SA60AT in 9 eyes, Sensar in 3 eyes, Tecnis 1 in 4 eyes, and Tecnis Toric in 2 eyes. The P_IOLadj is based on Gauss equations, using adjusted keratometric index (n_kadj) specific to keratoconus eyes. From this n_kadj, an adjusted keratometric corneal power is calculated (P_kadj). The P_IOLadj calculation was performed after estimating the effective lens position (ELP) using a mathematical expression obtained by multiple regression analysis (named ELP_adj). Comparison between the P_IOLadj and the real intraocular power implanted in each patient (P_IOLreal) was carried out.

Results: No significant differences between P_IOLreal and P_IOLadj were found. However, differences could be clinically relevant up to of 2.54 D as P_IOLreal increases. But, in the range of P_IOLreal between 0 and 20 D, differences were lower than 1.5 D, being most of them below 1 D.

Conclusion: A new formula of IOL power calculation (P_IOLadj) based on the use of an adjusted keratometric power (P_kadj) that considers a variable keratometric index due to the influence of the posterior corneal surface (n_kadj) and adjusted effective lens position (ELP_adj) is useful for estimating IOL power in low-to-moderate keratoconus, with more limitation in the most advanced keratoconus.

Keywords: Cataract, Intraocular lens calculation, Keratoconus.

INTRODUCTION

Some studies have evidenced that some errors are still possible in the calculation of intraocular lens power (P_IOL) in cataract surgery despite the technological advances and the latest formulas developed for such purpose^1–5 in healthy eyes (no pathological eye or with previous ocular surgeries). Classic keratometric corneal power (P_k), which is still used in some approaches for P_IOL calculation, assumes that the ratio between the anterior and posterior corneal curvature is constant. This approximation can lead to inaccuracies in corneal power estimation and therefore in the calculation of P_IOL. These errors can be increased significantly in keratoconus eyes due to the difficulty of determining the keratometric readings in such cases,^6–10 and the very significant variability of the ratio anterior/posterior corneal curvature in these eyes. It should be considered that the most important sources of errors in P_IOL calculation are the accuracy of the measurement of the axial length (AL), the estimation of the effective lens position (ELP), and the precision of the estimation of corneal power (P_c).¹ In clinical practice, total corneal power is still calculated by some practitioners only considering the anterior corneal surface and assuming a keratometric index (n_k). Several recalculations of n_k have been proposed to compensate for the keratometric corneal power estimation error.^11–16 It has been shown that the use of a single n_k value leads to an overestimation of corneal power in healthy corneas^{12,13,17–20} as well as in corneas after laser refractive surgery.^21–23 The same trend has been observed in keratoconus eyes,^24,25 with the error in corneal power estimation being dependent on the second corneal radius (r_2c).²⁵

Our research group proposed a variable keratometric index (n_kadj) depending on the radius of the anterior corneal surface (r_1c) as a valid option for minimizing the error associated with the keratometric approach for corneal power calculation in healthy eyes^19,20 and after laser refractive surgery when the technology for measuring the curvature of the posterior corneal surface is not available.^23,26 With the use of n_kadj, a new adjusted keratometric corneal power was defined (P_kadj). Comparing P_kadj with the corneal power obtained using the curvature of the two corneal surfaces (P_c^Gauss), the associated errors were below 0.5 D. Likewise, if the value of P_kadj was used in P_IOL calculation, the error associated was below 0.9 D.⁵ The same approach has been used in keratoconic eyes, and similar conclusion were obtained.²⁵ Specifically, eight different algorithms for n_kadj calculation according to the severity of keratoconus have been defined, with P_kadj minimizing the error associated with the use of the keratometric approach for corneal power calculation to a range within ±0.7 D.²⁴ Recently, new algorithms for n_kadj calculation have been also proposed for keratoconus eyes after corneal collagen crosslinking, also showing a minimization of the keratometric error in similar terms.²⁷

Concerning the impact of using the adjusted keratometric approach in P_IOL calculation, our research group confirmed that the use of the adjusted intraocular lens power (P_IOLadj) in healthy eyes for three different types of IOL would allow a minimization of the myopic residual trend occurring with these IOLs.^28–30 In these studies, a recalculation of ELP value, named adjusted ELP (ELP_adj), was necessary. Furthermore, in another previous study of our research group (currently in press), the differences in P_IOL calculation for four conventional IOL power formulas used in keratoconus eyes have been evaluated, confirming that the most comparable results are provided by the Hoffer Q and Holladay I formulas, whereas the Haigis formula provides the most discrepant outcome. In the same line of our previous investigations, the aim of the current study was to obtain an expression of P_IOLadj in keratoconus eyes associated with minimal errors in IOL power calculation.

MATERIALS AND METHODS

Patients

This retrospective study included a total of 25 eyes of 25 patients with ages ranging from 20 years to 76 years. All eyes had undergone cataract surgery with implantation of a monofocal spheric, aspheric, or toric IOL. Specifically, the following IOLs were implanted: Acrysof IQ Toric (Alcon Laboratories, Inc, Fort Worth, TX, USA), Acrysof SA60AT (Alcon Laboratories, Inc, Fort Worth, TX, USA) in 9 eyes, Sensar (Johnson and Johnson Vision, Santa Ana, CA, USA) in 3 eyes, Tecnis 1 (Johnson and Johnson Vision, Santa Ana, CA, USA) in 4 eyes, and Tecnis Toric (Johnson and Johnson Vision, Santa Ana, CA, USA) in 2 eyes. Inclusion criteria for this study were keratoconus eyes according to the standard diagnostic criteria that considers the presence of an asymmetric bow tie corneal topographic pattern with or without skewed axes, combined with at least one biomicroscopic sign, such as conical protrusion of the cornea at the apex, Vogt’s striae, stromal thinning, Fleischer ring, or anterior stromal scar,²⁵ and previous cataract surgery with implantation of a spheric or aspheric IOL, or even a toric IOL due to the presence of significant preexisting anterior corneal astigmatism. Exclusion criteria were patients with any other previous ocular surgery and eyes with other active pathologies different from keratoconus. All volunteers were adequately informed and signed a consent form following the tenets of the Helsinki declaration.

Surgery

All surgeries had been performed by the same experienced examiner using a standard technique of phacoemulsification under topical anesthesia and after pupillary dilation. After performing a corneal incision on the steepest meridian, a paracentesis 60°–90° clockwise from the main incision and the filling of the anterior chamber with viscoelastic material, the crystalline lens material was removed, and the IOL was implanted through the incision into the capsular bag using the specific injector developed by the manufacturer for each type of IOL. Finally, the surgeon proceeded to retrieve the viscoelastic material using the irrigation–aspiration system. A combination of topical steroid and antibiotic drops was prescribed to be applied four times daily for a week after the surgery and three times daily the second postoperative week.

Clinical Evaluation

A full ophthalmologic examination was performed in all cases, including manifest refraction, corrected distance visual acuity, slit-lamp biomicroscopy, Goldmann tonometry, fundus evaluation, and corneal analysis by a Scheimpflug photography-based tomography system (Pentacam system, software version 1.14r01, Oculus Optikgërate GmbH, Germany). Specifically, the following parameters were recorded and analyzed with the Pentacam system (see Table 1): anterior (r_1c) and posterior corneal radius (r_2c) in the central 3-mm corneal area, anterior and posterior corneal astigmatism (ACA and PCA, respectively), and minimum (MCT) and central corneal thickness (CCT).

Calculation of the Gaussian and Keratometric IOL Power

Almost all theoretical formulas for IOL power calculation are based on the use of a simplified eye model, with thin cornea and lens models.¹ According to this approach, the power of the IOL (P_IOL) can be easily calculated using the Gauss equations in paraxial optics:⁵

where P_c is the total corneal power, ELP is the effective lens plane, AL is the axial length of the eye, n_ha is the aqueous humor refractive index, n_hv is the vitreous humor refractive index, and R_des represents the postoperative desired refraction calculated at corneal vertex. The P_IOL estimation obtained using the keratometric corneal power (P_k) was defined as , whereas it was defined as when the Gaussian corneal power was used. The procedure of calculation of P_k, and had been described in detail in a previous article.^5,19

Calculation of the Adjusted Keratometric Index in Keratoconus Eyes

As in some of our previous studies,^19,20,23 the adjusted keratometric index (n_kadj) was defined as the value associated with an equivalent difference in magnitude between keratometric and Gaussian corneal power for extreme values of r_2c for each r_1c value.

In a recent study,²⁴ eight linear equations were defined for obtaining eight theoretical algorithms for the calculation of corneal power only depending on r_1c in keratoconus eyes. Specifically, the expressions shown in Table 1 was defined using the Gullstrand eye model.²⁴ Using this algorithm for estimating the most appropriate keratometric index to be used in each case, a new keratometric corneal power, named adjusted keratometric corneal power (P_kadj), was calculated using the classical keratometric approach for corneal power estimation without clinically relevant error.¹⁹ In the current study, an adjusted IOL power (P_IOLadj) was calculated, which was defined as the IOL power calculated from the eq. (1) using the n_kadj value for the estimation of the corneal power (P_kadj), as well as the n_ha and n_hv values corresponding to the Gullstrand eye model (1.336). In such calculation, the postoperative spherical equivalent at corneal vertex really obtained was considered as the desired refraction (R_des = SE_post). This adjusted IOL power (P_IOLadj) was compared with the real power of the IOL implanted (P_IOLReal). The P_IOLadj calculation was performed after estimating the ELP using a mathematical expression obtained by multiple regression analysis (named ELP_adj), as described in detail in the next section.

Estimation of Adjusted ELP by Multiple Regression Analysis

Considering in each patient the eq. (1), the values of P_IOLReal, P_kadj, and R_des = SE_post, ELP was estimated after clearing this term from the equation. This ELP value was designed as calculated ELP (ELP_calc). With the values of ELP_calc obtained in each eye included in the study, a multiple regression analysis was performed to obtain a mathematical expression predicting the best as possible the calculated ELP from different preoperative clinical data. This ELP was named adjusted effective lens position (ELP_adj). In addition, the ELP corresponding to each P_IOLReal was also calculated using the theoretical formula and was named as real effective lens position (ELP_Real). In this study, P_IOLReal was calculated using the Haigis, Hoffer Q, SRK/T and Holladay I formulas, all of them implemented in an Excel software sheet version 14.0.0 for Mac to obtain the corresponding ELP_Real.

Differences between the Adjusted and Real IOL Power Calculation Using the Adjusted Keratometric Index

The eight algorithms of Table 2²⁴ were applied for each patient to obtain n_kadj and its corresponding P_kadj. After this, P_IOLadj was calculated using the eq. (1), the n_kadj value for the estimation of corneal power (P_kadj), and the ELP value obtained by the linear regression equation predicting ELP (ELP_adj). After that, the difference (ΔP_IOL) between the adjusted (P_IOLadj) and the real IOL power (P_IOLReal) was also calculated as follows:

Statistical Analysis

The statistical analysis was performed using the SPSS statistics software package version 19.0 for Windows (IBM, Armonk, NY, USA). Normality of data samples was confirmed by means of the Shapiro–Wilk test. The Student’s t test was used for comparing the different approaches for ELP and P_IOL calculation. Differences were considered as statistically significant when the associated p < 0.05. Pearson coefficient was used to assess the correlation between ELP_adj and the ELP value calculated with the approach defined by each P_IOL calculation formula, as well as to assess the correlation between P_IOLadj and P_IOLReal. Regarding the analysis of the interchangeability between pairs of methods used for obtaining ELP and P_IOL, the Bland–Altman analysis was used.³¹ This is a graphical method for assessing if there is an agreement between two clinical procedures.³¹ The limits of agreement (LoA) are defined as the mean ±1.96 standard deviation (SD) of the differences.³¹ If the limits are clinically relevant, the 2 methods cannot be used interchangeably.

**Table 1**: Mean visual, refractive, biometric, and IOL power calculation data
Parameter	Mean ± SD	Range
SE_pre (D)	−5.5 ± 5.8	−15.0 to +10.0
SE_post (D)	−0.6 ± 0.9	−2.5 to +1.0
r_1c (mm)	7.43 ± 0.43	6.68 to 8.18
r_2c (mm)	6.10 ± 0.53	4.94 to 7.14
ACD (mm)	3.31 ± 0.54	2.00 to 4.05
AL (mm)	24.80 ± 2.49	20.77 to 30.64
ACA (D)	2.66 ± 2.02	0.30 to 8.70
PCA (D)	0.64 ± 0.44	0.10 to 2.50
n_kadj	1.329 ± 0.002	1.325 to 1.333
CCT (μm)	487 ± 43	390 to 570
P_kadj (D)	44.48 ± 2.53	40.62 to 48.95
P_c^Gauss (D)	44.31 ± 2.45	40.36 to 49.20
P_IOLReal (D)	15.22 ± 7.17	1.00 to 26.50

SE_pre and SE_post, pre- and postoperative spherical equivalent; r_1c and r_2c, radius of curvature of the anterior and posterior corneal surface, respectively; ACD, anterior chamber depth; AL, axial length; ACA and PCA, anterior and posterior corneal astigmatism; n_kadj, adjusted keratometric index; CCT, central corneal thickness; P_kadj, corneal power obtained using the adjusted keratometric index; P_c^Gauss, Gaussian corneal power; P_IOLReal, power of the intraocular lens implanted

**Table 2**: Algorithms of n_kadj developed using the Gullstrand eye model for different r_1c intervals
r_1c (mm)	n_kadj algorithm
(4.2, 4.7)	−0.01207 r_1c + 1.3789
(4.8, 5.6)	−0.01036 r_1c + 1.3787
(5.7, 6.2)	−0.00919 r_1c + 1.3785
(6.3, 6.4)	−0.00736 r_1c + 1.3782
(6.5, 6.8)	−0.00771 r_1c + 1.3783
(6.9, 7.5)	−0.00664 r_1c + 1.3780
(7.6, 7.8)	−0.00638 r_1c + 1.3781
(7.9, 8.5)	−0.00557 r_1c + 1.3779

A multiple regression analysis was used for predicting the ELP_adj from different preoperative anatomical and clinical parameters. Model assumptions were evaluated by analyzing residuals, the normality of nonstandardized residuals (homoscedasticity), and the Cook distance to detect influential points or outliers. In addition, the lack of correlation between errors and multicollinearity was assessed using the Durbin–Watson test, the calculation of the collinearity tolerance, and the variance inflation factor.

RESULTS

This study evaluated 25 eyes of 25 patients [13 women (52%)], with a mean range of 49.2 years ± 14.7 (SD) (range, 20–76 years). The sample comprised 13 right eyes (52%). Table 1 summarizes the preoperative visual, refractive, biometric, and IOL power calculation data of the eyes evaluated.

Estimation of ELP_adj

From the multiple regression analysis, the following expression for ELP_adj was obtained:

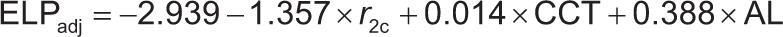
The multiple regression analysis revealed that the ELP_adj was significantly correlated with r_2c, CCT and AL (p < 0.001). The homoscedasticity of the model was confirmed by the normality of the nonstandardized residual distribution (p = 0.88) and the absence of influential points or outliers (mean Cook’s distance: 0.07 ± 0.13). With this model, 44% of nonstandardized residuals were lower than 0.5 and 80% were lower than 1.0. The poor correlation between residuals (Durbin–Watson test: 2.203) and the lack of multicollinearity (tolerance 0.670 to 0.894; variance inflation factors 1.493 to 1.144) was also confirmed. Table 3 shows the mean of the different values of ELP calculated in this study: adjusted, calculated, and real ELPs. As previously mentioned, ELP_calc was calculated considering the eq. (1), the values of P_IOLReal and P_kadj, and R_des = SE_post. ELP_Real was the value calculated with each theoretical formula used in each patient.

Agreement between ELP_adj and ELP_Real

No statistically significant differences were found between ELP_adj and ELP_Real (p = 0.785, Student’s t test). A moderate statistically significant correlation was found between ELP_adj and ELP_Real (r = 0.594, p < 0.01) (Fig. 1). According to the Bland–Altman method, the range of agreement between ELP_adj and ELP_Real was −0.06 mm, with limits of agreement of −2.12 and 2.01-mm. Figure 2 shows the Bland–Altman plot corresponding to this agreement analysis.

Agreement between P_IOLadj and P_IOLReal

As previously mentioned, P_IOLadj was calculated using the P_kadj value obtained in eq. (1) and the ELP_adj value obtained by the formula derived from multiple linear regression. No statistically significant differences were found between P_IOLadj (15.39 ± 7.09 D, range: 1.04 to 25.39 D) and P_IOLReal 15.22 ± 7.17 D, range: 1.00 to 26.50 D) when ELP_adj was used and R_des = SE_post was considered for P_IOLadj calculation (p = 0.49, Student’s t test). A very strong and significant correlation was found between P_IOLadj and P_IOLReal (r = 0.986, p < 0.01) (Fig. 3). According to the Bland–Altman method, the mean difference value between P_IOLadj and P_IOLReal was 0.17 D, with limits of agreement of −2.20 and +2.54 D (Fig. 4).

**Table 3**: Mean adjusted, calculated, and real effective lens position data
	Mean ± SD (mm)	Range (mm)	p value
ELP_Real	5.2787 ± 1.0511	3.4499–7.3643	0.69
ELP_adj	5.2706 ± 1.2518	3.2802–8.2640	0.27
ELP_calc	4.1535 ± 2.1422	−4.2937–8.3869	<0.001

Fig. 1: Relationship between the adjusted ELP (ELP_adj) and the real ELP estimated using the guidelines of the IOL power calculation formula used (ELP_real)

Correlation of ΔP_IOL with Other Clinical Variables

The correlations of ΔP_IOL with most of clinical variables evaluated were poor and did not reach statistical significance: r_1c (r = 0.08, p = 0.69), r_2c (r = 0.13, p = 0.53), CCT (r = −0.12, p = 0.57), AL (r = −0.08, p = 0.71), ACD (r = −0.19, p = 0.37), SE_preop (r = −0.03, p = 0.90), age (r = 0.31, p = 0.13), and P_kadj (r = −0.10, p = 0.65). A very poor but statistically significant correlation was found between ΔP_IOL and P_c^Gauss (r = −0.07, p < 0.01).

DISCUSSION

In this retrospective study with keratoconus patients, the potential validity of a new formula for IOL power calculation was evaluated (P_IOLadj), considering that the preoperative data and the real IOL power implanted (P_IOLreal) were known, as well as a new algorithm for ELP estimation (ELP_adj). Unlike a previous study was conducted by our research group to evaluate the potential usefulness of P_IOLadj in keratoconus,³² the current study is the first in comparing the outcomes of this formula with real retrospective data of cataract surgery. Although the results obtained with four different types of IOL were combined, a good correlation between P_IOLreal and P_IOLadj was found, with no significant differences between them. However, these nonstatistically significant differences were found to be clinically relevant (Fig. 4), increasing as the power of the implanted IOL increases, reaching a maximum value of 2.54 D. Specifically, differences between P_IOLreal and P_IOLadj were higher when the value of the P_IOLreal was higher than 20 D. However, in the range of P_IOLreal between 0 and 20 D, differences between P_IOLreal and P_IOLadj were lower than 1.5 D, being most of them below 1 D. These good results in this subgroup of patients may be due in part to the good correlation between ELP_real and ELP_adj, not finding statistically significant differences between them. According to the trend observed with the differences between P_IOLreal and P_IOLadj, higher differences between ELP_real and ELP_adj were also observed for eyes with high ELP values. Consequently, the development of future studies improving the precision of the algorithm to estimate ELP would allow a better prediction in cases requiring higher P_IOLadj values. Recently, Savini et al.³³ have demonstrated that cataract surgery results in keratoconus patients are worse in advanced stages of the disease. Possibly, in this series as well as in our population, the prediction of ELP in this type of patients is more difficult due to its variability with small variations of anatomical parameters. It should be considered that the distance between ELP and anterior IOL vertex position primarily depends on IOL power, IOL thickness, and shape factor,³⁴ and these factors are going to be significantly modified in eyes requiring high IOL powers.

Fig. 2: Differences between the adjusted effective lens position (ELP_adj) and the real effective lens position (ELP_real) plotted against the mean value of both. The upper and the lower lines represent the limits of agreement calculated as mean of differences ±1.96 SD

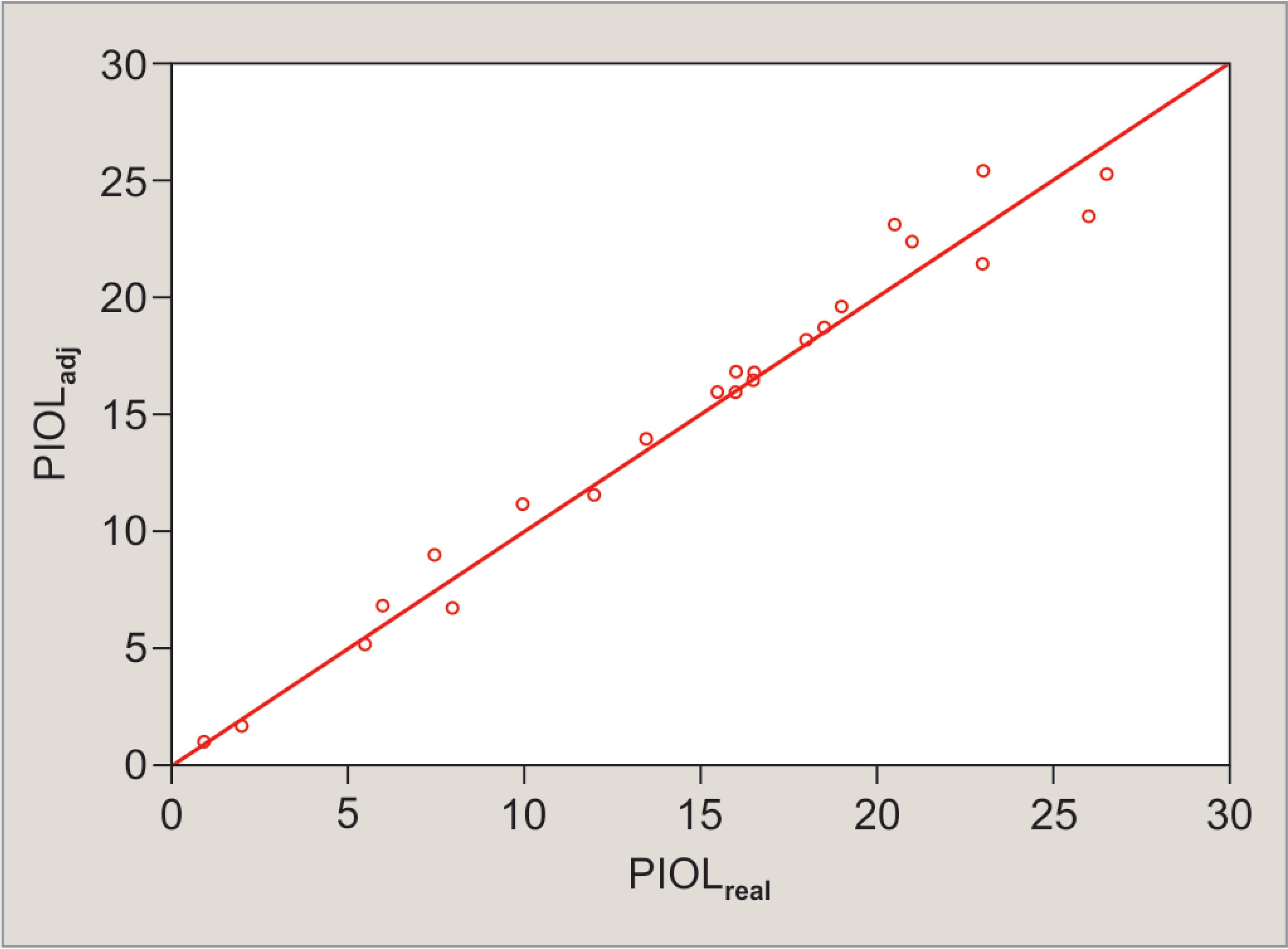
Fig. 3: Relationship between the adjusted (P_IOLadj) and the real intraocular lens power (P_IOLreal)

The approach for IOL power calculation evaluated in the current study allows the clinician to use the keratometric model based on the use of the curvature of the anterior corneal surface, but with a variable keratometric index for compensating the error rate associated with this approximation. Therefore, in keratoconus, the keratometric corneal power cannot be used as it is a source of significant clinical errors. The only acceptable relative simplification is the use of the adjusted keratometric approach in eyes with low to moderate keratoconus. Kamiya et al.³⁵ demonstrated that Sim K readings overestimate the corneal power, especially in advanced keratoconus, being this a possible source of hyperopic residual refractive error. Likewise, these same authors confirmed that a large amount of hyperopic shift occurred especially in advanced keratoconic patients, when keratometric readings were used for IOL power calculation, and that a slight, but significant, myopic shift occurred, when total corneal refractive power was used.⁶ Future studies should be performed to compare the results obtained with our IOL power approach compared to other algorithms for corneal power estimations and IOL power calculation formulas. Savini et al.³³ have recently demonstrated that the most accurate formula for IOL power calculation in keratoconus seems to be the SRK-T formula.

One additional finding confirming the validity of the adjusted keratometric approach evaluated in this study is that the difference between P_IOLreal and P_IOLadj did not correlate significantly with any anatomical preoperative parameter, suggesting that there is no factor limiting the prediction of IOL power based on our adjusted keratometric approach. In any case, it is important to mention that a low number of advanced keratoconus cases were included in our sample and possibly, as seen in the interchangeability analysis, parameters that are normally increased in advanced keratoconus may have correlated with the difference between P_IOLreal and P_IOLadj. This should be confirmed in future studies.

Fig. 4: Differences between the adjusted IOL power (P_IOLadj) and the real IOL power value implanted (P_IOLreal) plotted against the mean value of both. The upper and the lower lines represent the limits of agreement calculated as mean of differences ±1.96 SD

Concerning the limitations of the study, the most relevant is the sample size, which should be higher to conduct comparative studies with high levels of statistical power. However, this was not possible as this study was performed considering data obtained in the daily practice and the prevalence of keratoconus eyes undergoing cataract surgery is limited. This may be overcome with the performance of multicenter studies. Another limitation was the retrospective nature of the study. However, the results are quite consistent and can be used to guide future researches in this area.

In conclusion, a new formula of IOL power calculation (P_IOLadj) based on the use of an adjusted keratometric power (P_kadj) that consider a variable keratometric index due to the influence of the posterior corneal surface (n_kadj) and ELP_adj is useful for estimating IOL power in low to moderate keratoconus, with more limitation in the most advanced stages of the disease. Future prospective randomized comparative clinical trials should be conducted to consider the equivalence or superiority of this method of IOL power calculation compared to others.

COMPLIANCE WITH ETHICAL STANDARDS

Research Involving Human Participants and/or Animals

This article does not contain any studies with animals performed by any of the authors.

Informed Consent

Informed consent was obtained from all individual participants included in the study. All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.

REFERENCES

1. Olsen T. Calculation of intraocular lens power: a review. Acta Ophthalmol Scand 2007;85(5)472–485. DOI: 10.1111/j.1755-3768.2007.00879.x.

2. Narvaez J, Zimmerman G, Stulting RD, et al. Accuracy of intraocular lens power prediction using the Hoffer Q, Holladay 1, Holladay 2, and SRK/T formulas. J Cataract Refract Surg 2006;32(12):2050–2053. DOI: 10.1016/j.jcrs.2006.09.009.

3. Terzi E, Wang L, Kohnen T. Accuracy of modern intraocular lens power calculation formulas in refractive lens exchange for high myopia and high hyperopia. J Cataract Refract Surg 2009;35(7):1181–1189. DOI: 10.1016/j.jcrs.2009.02.026.

4. Zaldivar R, Shultz MC, Davidorf JM, et al. Intraocular lens power calculations in patients with extreme myopia. J Cataract Refract Surg 2000;26(5):668–674. DOI: 10.1016/S0886-3350(00)00367-9.

5. Camps VJ, Piñero DP, De Fez D, et al. Minimizing the IOL power error induced by keratometric power. Optom Vis Sci 2013;90(7):639–649. DOI: 10.1097/OPX.0b013e3182972f50.

6. Kamiya K, Iijima K, Nobuyuki S, et al. Predictability of intraocular lens power calculation for cataract with keratoconus: a multicenter study. Sci Rep 2018;8(1):1312. DOI: 10.1038/s41598-018-20040-w.

7. Leccisotti A. Refractive lens exchange in keratoconus. J Cataract Refract Surg 2006;32(5):742–746. DOI: 10.1016/j.jcrs.2006.01.063.

8. Thebpatiphat N, Hammersmith KM, Rapuano CJ, et al. Cataract surgery in keratoconus. Eye Contact Lens 2007;33(5):244–246. DOI: 10.1097/ICL.0b013e318030c96d.

9. Watson MP, Anand S, Bhogal M, et al. Cataract surgery outcome in eyes with keratoconus. Br J Ophthalmol 2014;98(3):361–364. DOI: 10.1136/bjophthalmol-2013-303829.

10. Park DY, Lim DH, Chung TY, et al. Intraocular lens power calculations in a patient with posterior keratoconus. Cornea 2013;32(5):708–711. DOI: 10.1097/ICO.0b013e3182797900.

11. Shammas HJ, Hoffer KJ, Shammas MC. Scheimpflug photography keratometry readings for routine intraocular lens power calculation. J Cataract Refract Surg 2009;35(2):330–334. DOI: 10.1016/j.jcrs.2008.10.041.

12. Ho JD, Tsai CY, Tsai RJ, et al. Validity of the keratometric index: evaluation by the pentacam rotating Scheimpflug camera. J Cataract Refract Surg 2008;34(1):137–145. DOI: 10.1016/j.jcrs.2007.09.033.

13. Borasio E, Stevens J, Smith GT. Estimation of true corneal power after keratorefractive surgery in eyes requiring cataract surgery: BESSt formula. J Cataract Refract Surg 2006;32(12):2004–2014. DOI: 10.1016/j.jcrs.2006.08.037.

14. Tang M, Li Y, Avila M, et al. Measuring total corneal power before and after laser in situ keratomileusis with high-speed optical coherence tomography. J Cataract Refract Surg 2006;32(11):1843–1850. DOI: 10.1016/j.jcrs.2006.04.046.

15. Gobbi PG, Carones F, Brancato R. Keratometric index, videokeratography, and refractive surgery. J Cataract Refract Surg 1998;24(2):202–211. DOI: 10.1016/S0886-3350(98)80201-0.

16. Dunne MC, Royston JM, Barnes DA. Normal variations of the posterior corneal surface. Acta Ophthalmol 1992;70(2):255–261. DOI: 10.1111/j.1755-3768.1992.tb04133.x.

17. Fam HB, Lim KL. Validity of the keratometric index: large population-based study. J Cataract Refract Surg 2007;33(4):686–691. DOI: 10.1016/j.jcrs.2006.11.023.

18. Olsen T. On the calculation of power from curvature of the cornea. Br J Ophthalmol 1986;70(2):152–154. DOI: 10.1136/bjo.70.2.152.

19. Camps VJ, Pinero Llorens DP, de Fez D, et al. Algorithm for correcting the keratometric estimation error in normal eyes. Optom Vis Sci 2012;89(2):221–228. DOI: 10.1097/OPX.0b013e31823ac694.

20. Piñero DP, Camps VJ, Mateo V, et al. Clinical validation of an algorithm to correct the error in the keratometric estimation of corneal power in normal eyes. J Cataract Refract Surg 2012;38(8):1333–1338. DOI: 10.1016/j.jcrs.2012.03.026.

21. Jin H, Holzer MP, Rabsilber T, et al. Intraocular lens power calculation after laser refractive surgery. Corrective algorithm for corneal power estimation. J Cataract Refract Surg 2010;36(1):87–96. DOI: 10.1016/j.jcrs.2009.07.011.

22. Liu Y, Wang Y, Wang Z, et al. Effects of error in radius of curvature on the corneal power measurement before and after laser refractive surgery for myopia. Ophthalmic Physiol Opt 2012;32(4):355–361. DOI: 10.1111/j.1475-1313.2012.00921.x.

23. Camps VJ, Piñero DP, Mateo V, et al. Algorithm for correcting the keratometric error in the estimation of the corneal power in eyes with previous myopic laser refractive surgery. Cornea 2013;32(11):1454–1459. DOI: 10.1097/ICO.0b013e31829e1eb5.

24. Camps VJ, Piñero DP, Caravaca-Arens E, et al. New approach for correction of error associated with keratometric estimation of corneal power in keratoconus. Cornea 2014;33(9):960–967. DOI: 10.1097/ICO.0000000000000190.

25. Piñero DP, Camps VJ, Caravaca-Arens E, et al. Estimation of the central corneal power in keratoconus: theoretical and clinical assessment of the error of the keratometric approach. Cornea 2014;33(3):274–279. DOI: 10.1097/ICO.0000000000000048.

26. Camps VJ, Piñero DP, Mateo V, et al. Clinical Validation of adjusted corneal power in patients with previous myopic lasik surgery. J Ophthalmol 2015;2015: 824293.

27. Piñero DP, Camps VJ, Caravaca-Arens E, et al. Algorithm for correcting the keratometric error in the estimation of the corneal power in keratoconus eyes after accelerated corneal collagen crosslinking. J Ophthalmol 2017;2017: 8529489.

28. Piñero D, Camps V, Ramón M, et al. Positional accommodative intraocular lens power error induced by the estimation of the corneal power and the effective lens position. Indian J Ophthalmol 2015;63(5):438–444. DOI: 10.4103/0301-4738.159882.

29. Piñero DP, Camps VJ, Ramón ML, et al. Error induced by the estimation of the corneal power and the effective lens position with a rotationally asymmetric refractive multifocal intraocular lens. Int J Ophthalmol 2015;8(3):501–507.

30. Piñero DP, Camps VJ, Ramón ML, et al. Preliminary evaluation of an algorithm to minimize the power error selection of an aspheric intraocular lens by optimizing the estimation of the corneal power and the effective lens position. Int Eye Sci 2016;16(6):1001–1008.

31. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986;1(8476):307–310. DOI: 10.1016/S0140-6736(86)90837-8.

32. Camps VJ, Piñero DP, Caravaca E, et al. Preliminary validation of an optimized algorithm for intraocular lens power calculation in keratoconus. Indian J Ophthalmol 2017;65(8):690–699. DOI: 10.4103/ijo.IJO_274_16.

33. Savini G, Abbate R, Hoffer KJ, et al. Intraocular lens power calculation in eyes with keratoconus. J Cataract Refract Surg 2019;45(5):576–581. DOI: 10.1016/j.jcrs.2018.11.029pii: S0886-3350(18)30968-4.

34. Schröder S, Langenbucher A. Relationship between effective lens position and axial position of a thick intraocular lens. PLoS ONE 2018;13(6): e0198824. DOI: 10.1371/journal.pone.0198824.

35. Kamiya K, Kono Y, Takahashi M, et al. Comparison of simulated keratometry and total refractive power for keratoconus according to the stage of Msler-Krumeich classification. Sci Rep 2018;8(1):12436. DOI: 10.1038/s41598-018-31008-1.

________________________
© The Author(s). 2019 Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and non-commercial reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.